Modeling COVID-19 disruptions via network mapping of the Common Core Mathematics Standards
Abstract
This paper develops a mathematical and computational modeling approach that provides a data-driven platform to address research questions relating to student pathways in K-12 education. Specifically, this paper uses scalable network modeling to create a model of the Common Core Mathematics Standards. The result is an educational map that formally represents the Standards and the relationships among them. This educational map is represented mathematically as a network model that forms the basis for computational graph analytics and visualization to identify Standards and learning pathways of interest. Using the network model, we model the disruption due to COVID-19 related school closures in Spring 2020. Analysis on the network model enables identification of propagating effects of the closures on later grades and reveals pathways with potential high vulnerability. When combined with school-specific and/or student data, this model could provide valuable analytics support to decision makers.
Keywords
Network modeling, Ontologies, Educational mapping, Intelligent tutoring systems, Common Core
1 Introduction
In the spring of 2020, millions of students abruptly shifted to online instruction, and in some cases, no instruction, as COVID-19 disrupted schools nationwide. But this disruption is not simply localized to a single semester: consider, for example, the downstream effects on a fifth grader, who needs to master adding fractions in order to perform more complicated operations in sixth and later grades. Failing to master an earlier, more fundamental learning outcome will result in difficulty mastering a learning outcome in a later grade that depends on the earlier outcome. It is critical to analyze such outcome dependencies in order to address learning gaps so that deficiencies are not propagated for years to come. To study these direct and indirect COVID-19 disruptions, this paper develops a graph-based, data-driven model of learning outcomes in a mathematics curriculum.
For our analysis to be widely applicable, we will consider the Common Core Mathematics curriculum. The Common Core Mathematics curriculum is a table list of 331 learning outcomes, dubbed “Standards”, for what students should be able to achieve in each grade band. The Common Core is standardized and adopted across 43 states in public school systems (National Governors Association Center for Best Practices Council of Chief State School Officers, 2010). It therefore facilitates a useful analysis that is widely applicable to all school systems who adopt the Common Core.
One major difficulty in analyzing chains of learning outcome dependencies is that of scale: if one is considering a single learning outcome and wishes to identify all downstream learning outcomes it may impact, including in later grades, it may be possible to trace and list all such downstream outcomes manually with some effort. However, such a process poses several issues. Firstly, it is difficult to replicate with the same result. Secondly, it is a manual and laborious process, with significant chance of oversight error. Thirdly, it does not allow for advanced analysis; for instance, manual lists make it difficult to denote a strong versus weak dependency and carry that forward in analysis. With these issues arising in analyzing a single outcome, how is it possible to analyze an entire curriculum of hundreds of learning outcomes?
The literature establishes the usefulness of mapping learning outcomes in a structured form and provides clues as to which structured form to use. Because we wish to analyze relationships, it is especially useful to look at network models, alternatively also referred to graph models. Courses have been linked in a curriculum through their learning outcomes in a graph-based model (Auvinen, 2011; Miller et al., 2016; Seering et al., 2015). Learning maps comprised of linked learning outcomes and activities have been created for adaptive learning (Bargel et al., 2012; Battou et al., 2011; Collins et al., 2005; Essa, 2016). Ontologies have also been created, visually linking topics, learning resources and other curriculum data in a diagram-like presentation (Bardet et al., 2008; Yudelson et al., 2015). More recently, Willcox and Huang (2017) introduced a network modeling framework for mapping educational data to leverage the unique relationship-first properties of graphs. Additional work referencing this network modeling approach includes graph-based visualization tools (Chen and Xue, 2018; Ghannam and Ansari, 2020; Samaranayake, 2019), curriculum development and design tools (Kaya, 2019), and adaptive learning tools (Cavanagh et al., 2019). We build upon this body of work by modeling the Common Core Mathematics Standards as a network model. To date, there has been limited research in structuring the Common Core in a network form. We emphasize the fact the Common Core Standards are presented as a list, devoid of any relationships. This is an acknowledged limitation since Standards are interrelated, and presenting them as a list loses important relationships (Daro et al., 2012; Zimba). Zimba presents the Common Core in a visual diagram with connections amongst Standards. However, as it only presents a visual diagram without an underlying network model, it is of limited analytic use. We go further by developing a structured, data-driven network model and using it to generate replicable analyses and visualizations. We chunk Standards into finer-grained statements of skills mastery, dubbed “Micro-Standards”, and we draw prerequisite connections between Micro-Standards. In doing so, we rely on an established body of work in using experts to identify prerequisites within a hierarchy of skills (Cotton et al., 1977; White, 1974; Gagne and Paradise, 1961; Liang et al., 2017; Wang et al., 2016). By drawing prerequisite linkages between Micro-Standards (finer-grained skills) rather than just Standards (coarser-grained skills), we enable greater precision in relationships between statements of skills mastery (Popham, 2006; Pardos et al., 2006; Huang and Willcox, 2021). This higher level of granularity is a crucial requirement in many use cases (McCalla and Greer, 1994; Greer and McCalla, 1989; Hobbs, 1985), such as curating reusable repositories of learning content 1, designing just-in-time interventions to address micro-sized learning targets (Gagne et al., 2019), intelligent tutoring systems that serve adaptive assessments to students (Huang and Willcox, 2021), etc.
In this paper, we develop a network model for the Common Core Mathematics curriculum and use it to analyze COVID-19 disruptions. The next section presents the theoretical network model. We then illustrate mapping the Common Core curriculum into a network structure, including the process of discretizing Common Core Standards into Micro-Standards and creating prerequisite linkages. With the resulting network map, we identify vertices and pathways of interest. We then model the Spring 2020 COVID-19 school closures as a shock to the system, with specific Micro-Standards initially impacted. Using graph analysis, we trace the propagating effects of the initial shock to later grades. Our analysis shows far-reaching consequences of COVID-19 disruptions and reveals learning pathways of interest. Finally, we discuss the analytic and predictive power obtained by our Common Core network model versus that of the classic Common Core Standard list.
2 The Network Model
A network model is a set of entities and relationships arranged in a graph structure in which entities are represented as vertices, or nodes, and relationships are represented as edges between vertices. Examples of entities include: educational institutions, departments, subjects, learning modules, topics, learning outcomes, etc. Examples of relationships include: prerequisite links between any two learning outcomes, parent-child relationships that denote categorical groupings, etc.
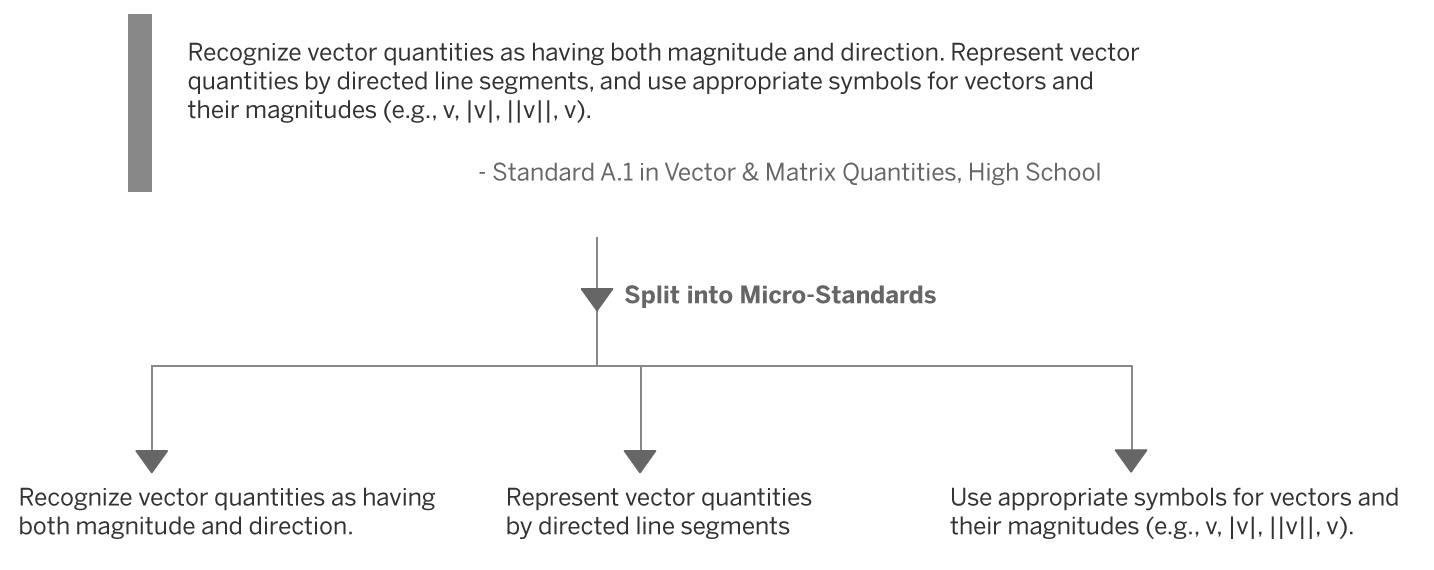
In the network model developed in this paper, we define the notion of a Micro-Standard entity. Readers familiar with the Common Core will know that the Common Core defines “Standards”, medium-grained statements of skills mastery. Our defined Micro-Standards are more fine-grained statements, derived from dividing up a Standard. For instance, Figure 1 shows a Standard that has been divided up into three Micro-Standards, resulting in highly specific statements of skills mastery.
We then define a has-prerequisite-of relationship that points from one Micro-Standard to the next Micro-Standard. This relationship represents the notion that mastering one Micro-Standard is necessary in order to master the next Micro-Standard. Prerequisite relationships between Standards are implied in the Common Core Standards. For instance, in order to add, “Subtract and multiple complex numbers,” it is naturally obvious that a learner must first be able to define what a complex number is. By defining these has-prerequisite-of relationships, we make relationships explicit and designate them as first-class objects in the network model. As discussed in Cotton et al. (1977); Collins et al. (2005), the identification of prerequisites between entities is sensitive to the granularity of the entities — the coarser the statement of learning, the more dimensions for interpretation there are as to what constitutes a prerequisite. By drawing has-prerequisite-relationships between Micro-Standards, we inject more granularity and precision into the model because we can narrow in exactly on why a prerequisite linkage is justified.
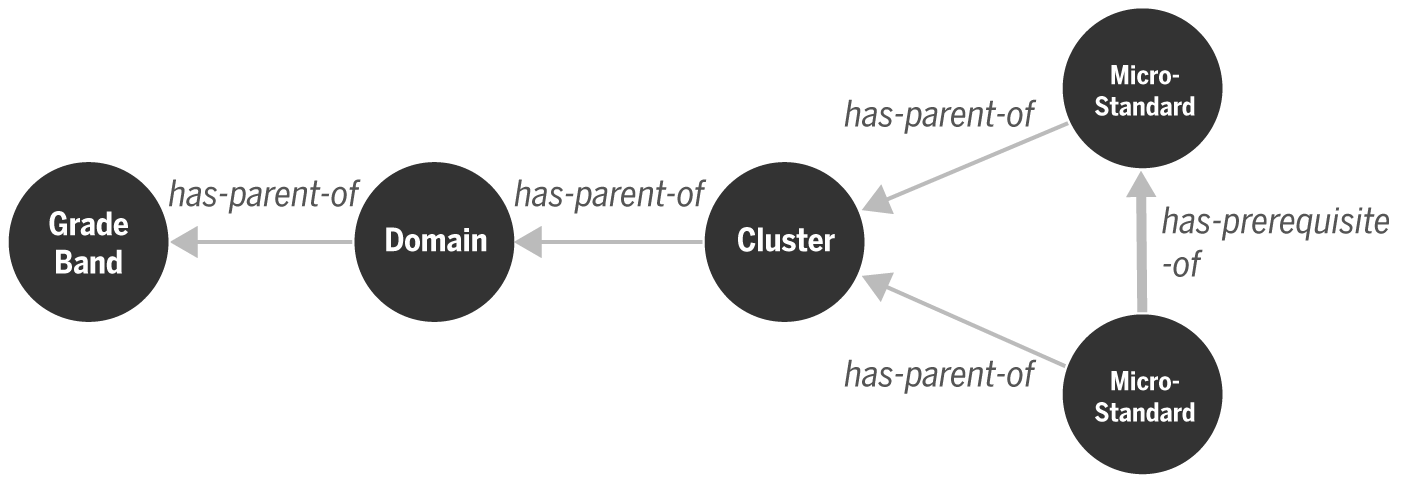
We define the remaining entities in our model: Cluster, Domain and Grade Level / Band. These entities correspond to how Standards are grouped in the Common Core: a Cluster is a grouping of Micro-Standards, a Domain is a grouping of Clusters, and a Grade Band is a grouping of Domains. To model such a notion of grouping, we further define a has-parent-of relationship pointing from the child entity to the parent group entity. Figure 2 shows a schematic of the resulting network model.
We briefly introduce several basic concepts of graph theory that we will use to analyze the Common Core curriculum network. The in-degree of a vertex is the number of incoming edges; the out-degree of a vertex is the number of outgoing edges. The Common Core network model belongs to a special class of graphs called directed acyclic graphs (DAG) in which there are no cycles in the graph. For DAGs, one can compute a topological sort of the vertices such that there is no edge going from any vertex in the sorted sequence to an earlier vertex in the sequence. Within the topological sort, we can rank vertices such that the of a vertex is the longest path from some source vertex to .
3 Mapping the Common Core
The Common Core Mathematics Area comprises 331 Standards across ten grade bands from Kindergarten through High School. Standards are medium-grained statements of skills mastery. From Kindergarten through Grade 8, Standards are grouped into Domains. In the High School grade band, Standards are grouped under Clusters, and Clusters are further grouped by Domains. As an example, Table 1 illustrates a set of Standards in the “Vector & Matrix Quantities” Cluster, further nested under the “Number & Quantity” Domain in the High School grade band.
| Domain: Vector and Matrix Quantities |
| Cluster: Represent and model with vector quantities |
| A.1 Recognize vector quantities as having both magnitude and direction. Represent vector quantities by directed line segments, and use appropriate symbols for vectors and their magnitudes (e.g., , , , ). |
| A.2 Solve problems involving velocity and other quantities that can be represented by vectors. |
| A.3 Find the components of a vector by subtracting the coordinates of an initial point from the coordinates of a terminal point. |
| Cluster: Perform operations on vectors. |
| B.4.A Add vectors end-to-end, component-wise, and by the parallelogram rule. Understand that the magnitude of a sum of two vectors is typically not the sum of the magnitudes |
| B.4.A Given two vectors in magnitude and direction form, determine the magnitude and direction of their sum |
| ⋮ |
|
|
To create Micro-Standards, we divide a Standard into finer-grained statements of skills mastery. To do this, we determine whether a Standard contains multiple discrete skills. In the interests of preserving fidelity, this determination was largely based on grammatical clues, such as periods, semi-colons separating independent clauses, numbered points, etc. In all cases, we attempted to preserve the original wording of a Standard and did not introduce new meaning when splitting it into discrete statements. For instance, in Figure 1, Standard A.1 has two complete sentences with one independent clause. We split this Standard to create three distinct Micro-Standards with original wording: “Represent vector quantities as having both magnitude and direction” is a distinct skill from being able to “Represent vector quantities by directed line segments,” which is yet distinct from “Use appropriate symbols for vectors and their magnitudes.” The figure illustrates a Standard broken into three Micro-Standards. Dividing up Standards in this way results in finer-grained entities that drive more powerful analytics and precise analysis.
The next step in creating the network model is to draw prerequisite relationships between Micro-Standards. Focusing on one grade band at a time, we review the Micro-Standards within the given grade band. We determine whether a given Micro-Standard is a prerequisite to another Micro-Standard via a top-down decomposition with subject matter experts established in literature (Cotton et al., 1977; White, 1974; Gagne and Paradise, 1961). These subject matter experts are active researchers in the field of education and mathematics. We first identify (within a grade band) a candidate set of the most synthesizing skills — that is, the skills that build upon the most prior skill. For each Micro-Standard in the candidate set, we then identify the immediate Micro-outcomes within that grade band that are necessary for learning the synthesizing Micro-Standard. We thus create the prerequisite relationships between the target synthesizing Micro-Standard and the prerequisite Micro-Standards. Next, we take the previously-identified prerequisite Micro-Standards and in turn identify their prerequisites. Note that we draw only direct prerequisite relationships: that is, if Micro-Standard A requires Micro-Standard B, and Micro-Standard B requires C, we draw a relationship between A and B, and a relationship between B and C, but we do not draw a relationship between A and C. This level by level decomposition is a breadth-first traversal and gives us a tentative version of the partial dependency tree. Because this initial version was formed by one subject matter expert, we check the reasonableness of the dependencies by polling at least two other subject matter experts. Any revisions are agreed upon in consensus. In this way, we progress through all the grade bands, constructing the intra-grade prerequisite relationships.
After the intra-grade prerequisite relationships are constructed, we step through the grades again to draw inter-grade prerequisite relationships. Starting from the most downstream grade band (i.e., the High School grade band), we identify the most fundamental Micro-Standards in a given Cluster or Domain, i.e., the Micro-Standards that do not have any intra-grade prerequisites. We then identify any prerequisites in the previous grade band; if none can be found in the immediate preceding grade band, we step back to the next preceding grade band and begin the search again. After every grade band iteration, we again check for consensus amongst experts in the updated linkages. In this way, we step through all the grade bands and construct inter-grade prerequisite relationships.
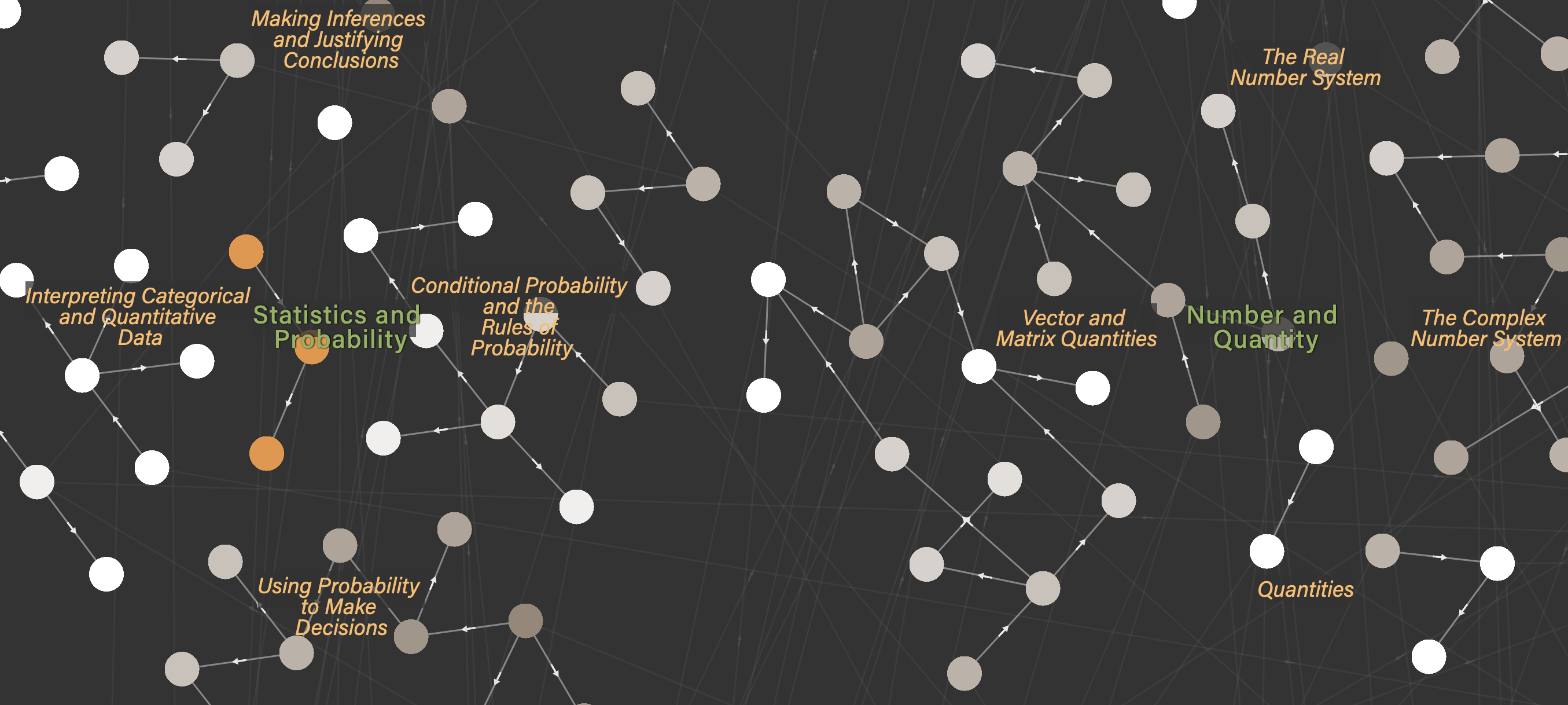
Table 2 shows the total number of mapped entities and relationships for the Common Core. Figure 3 shows a zoomed-in visualization of the resulting network map of Micro-Standards grouped within several Clusters and two Domains in the High School grade band.
With the resulting network map, we can analyze the curriculum for Micro-Standards of interest. Table 3 shows some example graph analytics. Across all grade bands, the vertex with the highest in-degree is that of Micro-Standard 4.NBT.1 Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right. That is, Micro-Standard 4.NBT.1 has the highest number of adjacent follow-on Micro-Standards in our network model of the Common Core. There are five vertices that tie for the highest out-degree (i.e., they are the Micro-Standards that have the highest number of direct pre-requisite Micro-Standards in our network model). Table 3 lists these as Micro-Standards 1.0A.6, 2.0A.2, 3.OA.7, 3.OA.9, and G-CO.4 in grades 1, 2, 3, 3, and High School, respectively. This kind of analysis provides insight into the elements of the curriculum that have the potential for causing or experiencing large disruption.
| Metric | Micro-Standard | Grade |
| Highest in-degree | 4.NBT.1 Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right. | 4 |
| Highest out-degree | 1.0A.6 Add and subtract within 20; 2.0A.2 Fluently add and subtract within 20; 3.OA.7 Fluently multiply & divide within 100; 3.OA.9 Identify arithmetic patterns; G-CO.4 Develop definitions of rotations, reflections, and translations | 1; 2; 3; 3; |
| Highest incoming rank | 9 (17 vertices) |
|
| Highest outgoing rank | 9 (6 vertices) |
|
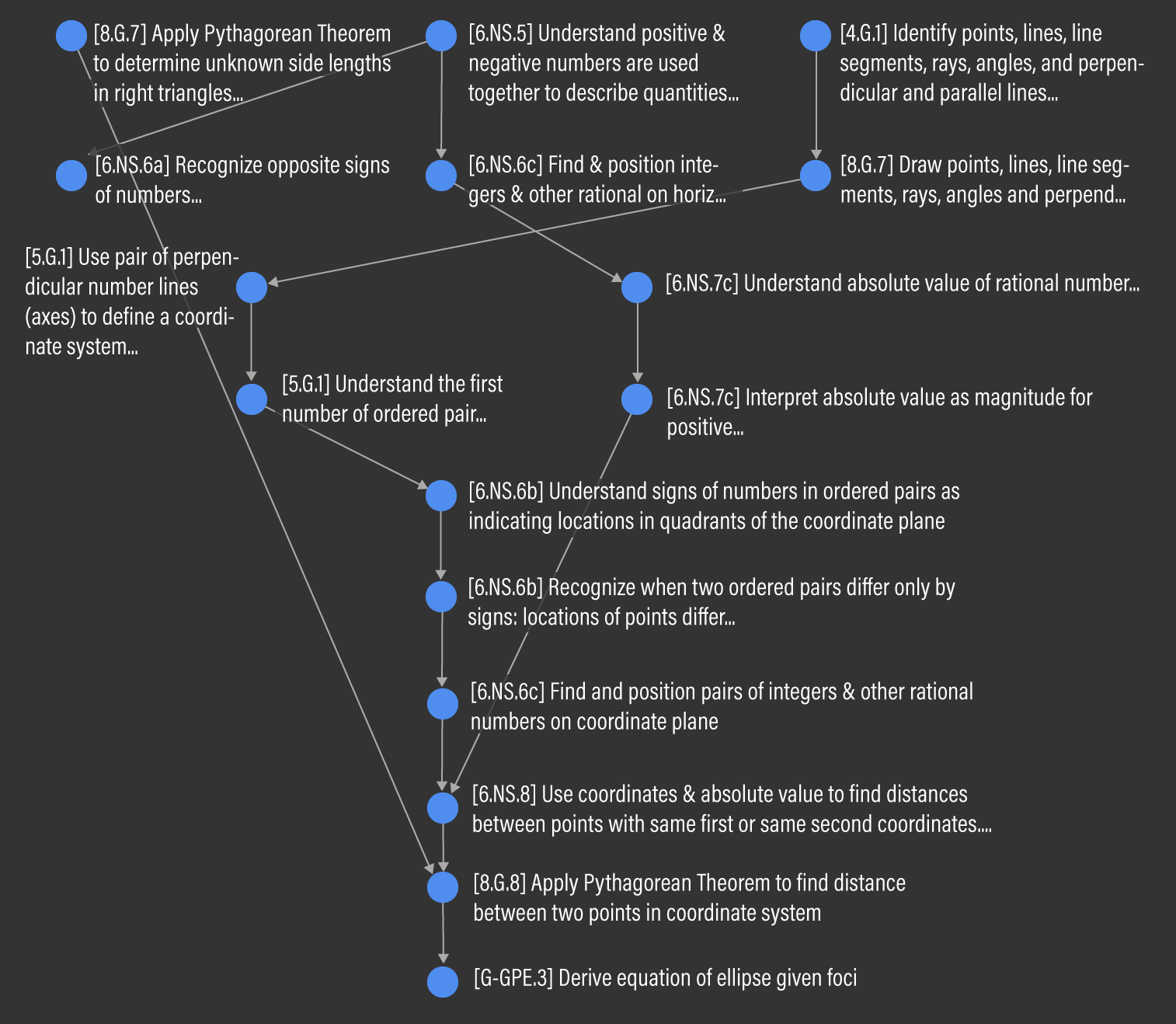
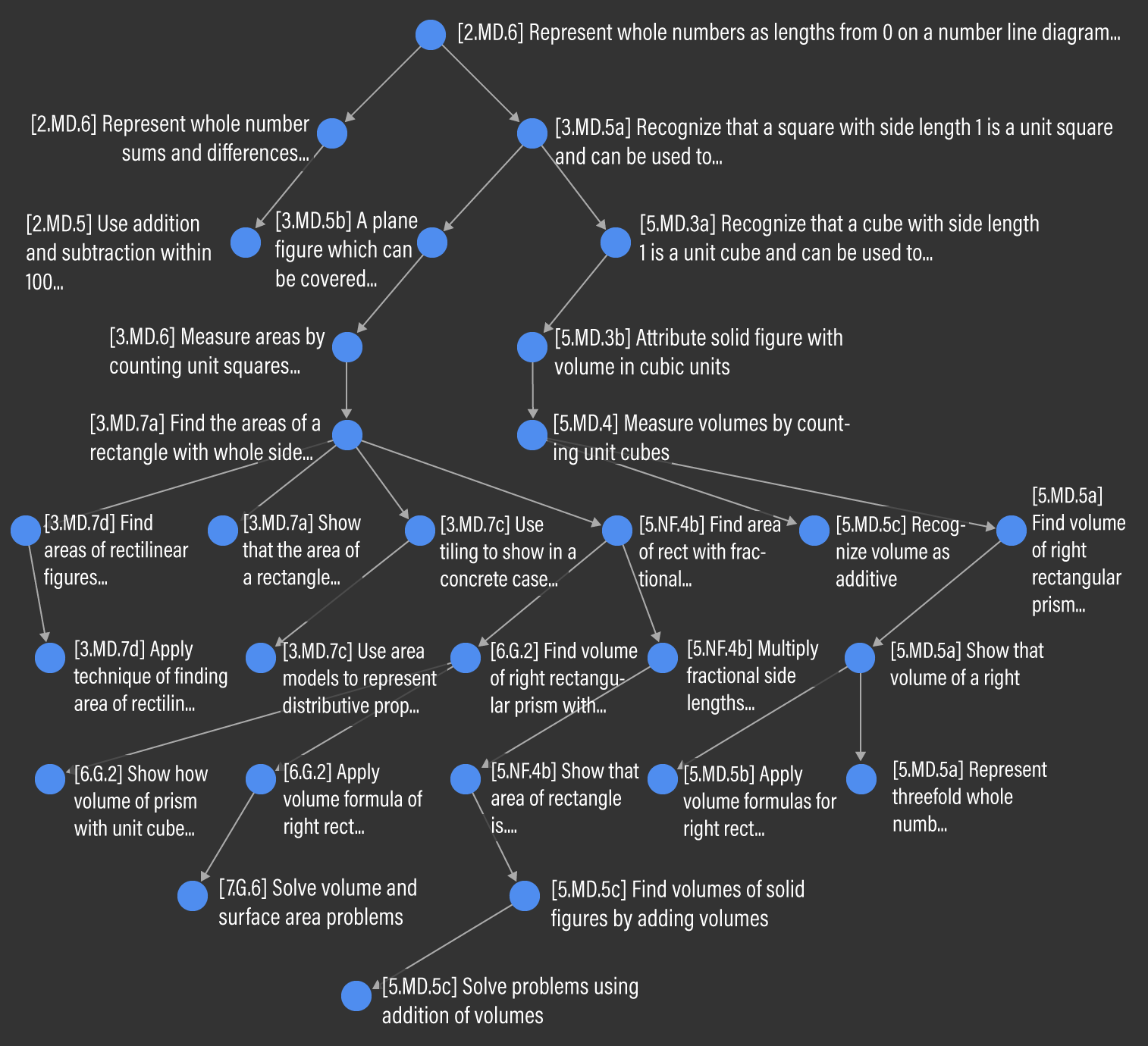
Finally, we conduct a topological sort of the entire Common Core Mathematics curriculum to look at learning pathways of interest. Of particular interest are learning pathways that are especially long, since these pathways may be highly vulnerable to disruption. These pathways can be found by tracing the vertices with the highest rank in both the incoming and outgoing directions. A total of 17 vertices tie for the highest outgoing rank of nine. For example, G-GPE.3 Derive the equation of an ellipse given the foci in High School has a prerequisite path length of nine; Figure 4 visualizes this path. Note that in our visualization, arrows point from a more fundamental Micro-Standard to a downstream one, since it is more intuitive to visualize learning flow in this direction. This is in contrast to the underlying mathematical model depicted in Figure 2, where the directed has-prerequisite-of edge in the graph points from the downstream Micro-Standard to its prerequisite. Six vertices tie for the highest incoming rank of nine. For example, 2.MD.6 Represent whole numbers as lengths on a number line in Grade 2 leads to a downstream path of length nine, across four grade bands. This branching pathway is visualized in Figure 5.
4 Example Application: COVID Disruption in Massachusetts
The resulting network map represents a structured view of how learners move through the Common Core Mathematics curriculum. With this network model, we can follow learning paths, assign probabilities or weights to the edges between vertices, and replicate our analyses. As one application example, we analyze the disruptions caused by school closures on March 15, 2020 in Massachusetts. From March 15 to the end of the school year, schools were either entirely closed or had adopted online learning in Massachusetts. In our example analysis, we consider any Micro-Standard scheduled to be taught during this time to have been disrupted.
For every Micro-Standard that was directly impacted during this time, we assign the vertex a boolean attribute of directly_impacted = true and color that vertex red for visual illustration. For each Micro-Standard that was directly impacted, we follow incident incoming edges of type has-prerequisite-of to arrive at other vertices of type Micro-Standard that depend on the impacted Micro-Standard. Formally, we conduct a breadth-first search to discover the Micro-Standards in order of ascending immediacy: the immediate neighbors of the initial vertex are the next Micro-Standards to be disrupted; the neighbors of these next Micro-Standards are further next in line, and so forth. We assign these downstream vertices a boolean attribute of indirectly_impacted=true and color them yellow. We note that our modeling approach is not limited to boolean attributes as used here; vertices can be attached different types of values such as continuous probability values, categorical values, discrete values, etc.
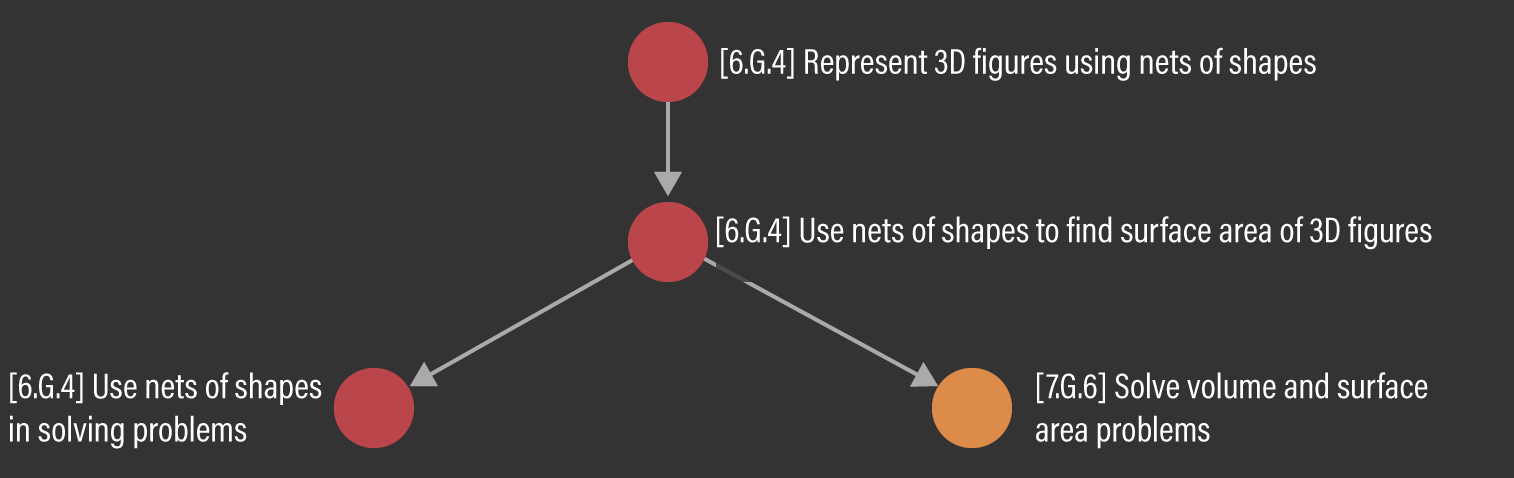
In one analysis, we analyze the downstream impact to sixth graders. Using the sixth grade syllabus of Cambridge Public Schools (Cambridge Public Schools, 2015), we estimated there was a total of 27 Micro-Standards scheduled to be taught during the period of school closures. To show some examples of pathway analyses: Figure 6 illustrates a path of a single directly-impacted Micro-Standard, 6.G.4, colored red, located at the top of the figure. This Micro-Standard leads to 6.G.4, another directly-impacted Micro-Standard, which leads to 7.G.6, a downstream-impacted Micro-Standard in the seventh grade. In this simple example, we observe how one directly-impacted Micro-Standard in the sixth grade leads to a downstream disruption of one Micro-Standard in the seventh grade.
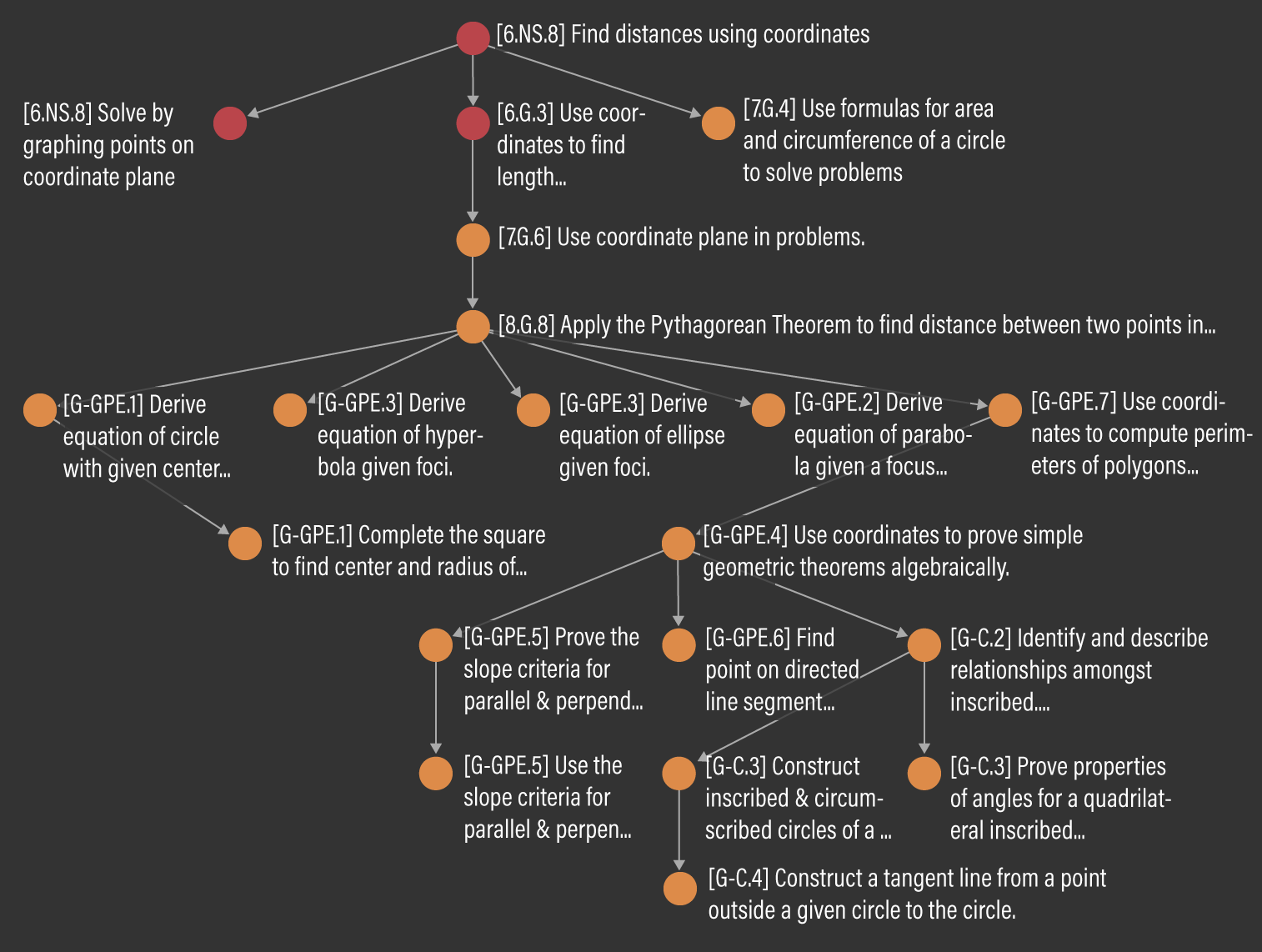
In another more complex example: Figure 7 traces the downstream path of a single directly-impacted Micro-Standard, 6.NS.8, colored in red, located at the top of the figure. 6.NS.8 has three immediate downstream Micro-Standards: 6.NS.8, 6.G.8, and 7.G.4. While both 6.NS.8 and 6.G.3 were scheduled to be taught during school closures and are thus directly impacted, 7.G.4 was not scheduled to be taught during that time. 7.G.4 is in fact a Micro-Standard taught in the seventh grade. 7.G.4 leads to another Micro-Standard in the seventh grade, 7.G.6, which in turn leads to an eighth grade Micro-Standard 8.G.8. 8.G.8 has five immediate downstream Micro-Standards: G-GPE.1, G-GPE.3, G-GPE.3, G-GPE.2 and G-GPE.7. These five Micro-Standards are all located in the High School grade band and they lead to even more downstream Micro-Standards. In this example, we observe that a single Micro-Standard impacted 17 downstream Micro-Standards spanning three grade bands. Our sixth grade analysis showed that from an initial 27 Micro-Standards, there resulted a total of 37 downstream impacted Micro-Standards, spanning a total of four grade bands. Note that because the High School grade band is counted as a single grade band, more than four grades are likely to have been impacted. All disrupted outcomes in this example are listed in Table 4.
5 Discussion
In mapping the Common Core Mathematics Standards, our process of chunking Standards and identifying linkages between the resulting Micro-Standards requires some level of subjective input. In chunking the Standards, we attempted to preserve the original wording as closely as possible and used grammatical hints such as periods, independent clauses, etc. to divide up Standards. This process of dividing up Standards not only achieves improved uniformity with respect to grain size across Micro-Standards, but also enables more precise relationships between Micro-Standards to be drawn. Even with a panel of subject matter experts, there is unlikely to be complete agreement on all prerequisite relationships; the results presented here based on our own modeling of the relationships are intended to be illustrative. Even if the modeling approach highlights points of disagreement and/or multiple potential prerequisite paths, this in itself could be a useful outcome. Further revision of linkages between Micro-Standards is an ongoing and future undertaking. We note that because we leveraged network models in which relationships are first-class objects, it is a straightforward task to re-run analyses after entities and relationships are edited.
In drawing relationships between Micro-Standards, we acknowledge that there may be missing or extraneous linkages. This is an issue that will be present for any model representing a complex dataset. However, the power of our graph model approach is such that irrelevant links can be surfaced and discarded, and missing links can be revealed when one layers in student activity data. For example, with the incorporation of student activity into the graph model, we can observe which linkages are indeed relevant or missing, and prune and add as needed. In addition, we have simplified linkages to boolean values — either an edge exists or it does not. It is straightforward to expand the model so that edges admit numerical weights to indicate the strength of the relationship between two Micro-Standards (although assigning these weights will again require subjective expert input). For instance, the numerical strength of a relationship can be a result of a panel vote of experts or even an algorithmically-derived value from application of machine learning. In our particular COVID-19 application case, assigning edge weights will lead to non-boolean determinations for whether downstream Micro-Standards are impacted and is an area of future work.
The mapped network form of the Common Core Mathematics curriculum yields important insights not obtainable with its classic list form. Vertices with high in-degrees are important since they represent Micro-Standards upon which many other Micro-Standards rely. Disruption to achieving high in-degree Micro-Standards will lead to many failures downstream. Vertices with high out-degrees represent the Micro-Standards most sensitive to disruption, as they rely on a great amount of prerequisite mastery. Also of interest are long paths: when Micro-Standards require the learner to retrieve knowledge from a long time ago, there may be greater chance of failure. Long learning paths indicate that additional support may be needed, such as just-in-time interventions. For instance, Essa (2016) proposes an adaptive learning framework with granular learning objects that serve to surface just-in-time actionable insights and feedback. These observations are important for curriculum design under normal circumstances, but become critical in a crisis situation such as COVID-19 when learning is widely disrupted. In this paper, we have chosen a particular grade and state to introduce the initial COVID-19 shock. We emphasize that our data-driven network model enables rapid and scalable analyses under different inputs, such as choosing an earlier grade.
The graph analysis conducted in this paper is illustrative and does not represent the full capability of the network model, nor its significance for curriculum design and adaptive learning applications. There is much scope for further analysis. For instance, graph partition analysis can be useful for discovering and designing parallel tracks of study. A learner model can be superimposed over the base network map to track how individual learners progress through the curriculum. While other studies have visualized the Common Core form with linkages (Zimba), to our knowledge, this is the first study to formally construct a network model of the Common Core and unlock graph-based analysis techniques.
6 Conclusion
We present a data-driven graph-based approach for modeling the Common Core Mathematics curriculum. Our main result is that the network structure makes possible scalable analysis in tracing relationships and effects in learning paths in the Common Core Math Standards. Using COVID-19 school closures in spring 2020 as an initial shock, we trace the propagating effects in the network starting in sixth grade reaching through high school. Because our approach includes first discretizing the Common Core Standards into more fine-grained statements of skills mastery, we are able to identify with a higher level of precision which Micro-Standards will experience disruption. We have not validated our predictions against student assessment data given ongoing COVID-19 conditions, but our main result reveals vulnerable learning pathways to investigate. Validation constitutes an important area for future research. Finally, we note that in the process of validation there must be necessary revisions, and an important advantage of our network modeling approach is that our graph structure enables easy revision of vertices and edges.
Data access
We make the mapped network dataset publicly available via API access at the MIT Mapping Lab (https://mapping.mit.edu).
| |
|||
| No. |
Outcome |
Impact Type | Grade |
| 1. |
[6.EE.2c] Evaluate expressions at specific values of their variables. |
Directly-impacted | Grade 6 |
| 2. |
[6.EE.2c] Perform arithmetic operations, including those involving whole number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations). |
Directly-impacted | Grade 6 |
| 3. |
[6.EE.5] Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? |
Directly-impacted | Grade 6 |
| 4. |
[6.EE.5] Use substitution to determine whether a given number in a specified set makes an equation or inequality true. |
Directly-impacted | Grade 6 |
| 5. |
[6.EE.7] Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px = q for cases in which p, q and x are all nonnegative rational numbers. |
Directly-impacted | Grade 6 |
| 6. |
[6.EE.8] Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. |
Directly-impacted | Grade 6 |
| 7. |
[6.EE.8] Recognize that inequalities of the form x > c or x < c have infinitely many solutions |
Directly-impacted | Grade 6 |
| 8. |
[6.EE.8] Represent solutions of inequalities x > c or x < c on number line diagrams. |
Directly-impacted | Grade 6 |
| 9. |
[6.EE.9] Use variables to represent two quantities in a real-world problem that change in relationship to one another |
Directly-impacted | Grade 6 |
| 10. |
[6.EE.9] Write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. |
Directly-impacted | Grade 6 |
| 11. |
[6.EE.9] Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation. |
Directly-impacted | Grade 6 |
| 12. |
[6.G.1] Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes |
Directly-impacted | Grade 6 |
| 13. |
[6.G.1] Apply techniques that find the area of polygons by composing into rectangles or decomposing into triangles in the context of solving real-world and mathematical problems. |
Directly-impacted | Grade 6 |
| 14. |
[6.G.2] Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths |
Directly-impacted | Grade 6 |
| 15. |
[6.G.2] Show that the volume of a right rectangular prism with fractional edge lengths is the same as would be found by multiplying the edge lengths of the prism. |
Directly-impacted | Grade 6 |
| 16. |
[6.G.2] Apply the formulas V = l w h and V = b h to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems. |
Directly-impacted | Grade 6 |
| 17. |
[6.G.3] Draw polygons in the coordinate plane given coordinates for the vertices |
Directly-impacted | Grade 6 |
| 18. |
[6.G.3] Use coordinates to find the length of a side joining points with the same first coordinate or the same second coordinate |
Directly-impacted | Grade 6 |
| 19. |
[6.G.3] Apply techniques of drawing on the coordinate plane and finding side lengths in the context of solving real-world and mathematical problems. |
Directly-impacted | Grade 6 |
| 20. |
[6.G.4] Represent three-dimensional figures using nets made up of rectangles and triangles |
Directly-impacted | Grade 6 |
| 21. |
[6.G.4] Use the nets made up of rectangles and triangles to find the surface area of these figures. |
Directly-impacted | Grade 6 |
| 22. |
[6.G.4] Apply techniques using nets made up of rectangles and triangles in the context of solving real-world and mathematical problems. |
Directly-impacted | Grade 6 |
| 23. |
[6.NS.8] Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. |
Directly-impacted | Grade 6 |
| 24. |
[6.NS.8] Use coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate. |
Directly-impacted | Grade 6 |
| 25. |
[6.SP.1] Recognize a statistical question as one that anticipates variability in the data related to the question and accounts for it in the answers. |
Directly-impacted | Grade 6 |
| 26. |
[6.SP.2] Understand that a set of data collected to answer a statistical question has a distribution which can be described by its center, spread, and overall shape. |
Directly-impacted | Grade 6 |
| 27. |
[6.SP.3] Recognize that a measure of center for a numerical data set summarizes all of its values with a single number, while a measure of variation describes how its values vary with a single number. |
Downstream impacted | Grade 6 |
| 28. |
[6.SP.4] Display numerical data in plots on a number line, including dot plots, histograms, and box plots. |
Directly-impacted | Grade 6 |
| 29. |
[6.SP.5a] Summarize numerical data sets in relation to their context by reporting the number of observations. |
Downstream impacted | Grade 6 |
| 30. |
[6.SP.5c] Summarize numerical data sets in relation to their context by giving quantitative measures of center (median and/or mean) and variability (interquartile range and/or mean absolute deviation) |
Downstream impacted | Grade 6 |
| 31. |
[6.SP.5c] Summarize numerical data sets by describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered. |
Downstream impacted | Grade 6 |
| 32. |
[6.SP.5d] Summarize numerical data sets in relation to their context by relating the choice of measures of center and variability to the shape of the data distribution and the context in which the data were gathered. |
Downstream impacted | Grade 6 |
| 33. |
[7.G.1] Solve problems involving scale drawings of geometric figures. |
Downstream impacted | Grade 7 |
| 34. |
[7.G.4] Use the formulas for the area and circumference of a circle to solve problems. |
Downstream impacted | Grade 7 |
| 35. |
[7.G.6] Solve real-world and mathematical problems involving area of 2-D objects |
Downstream impacted | Grade 7 |
| 36. |
[7.G.6] Solve real-world and mathematical problems involving volume and surface area of 3-D objects. |
Downstream impacted | Grade 7 |
| 37. |
[7.SP.1] Understand that statistics can be used to gain information about a population by examining a sample of the population. |
Downstream impacted | Grade 7 |
| 38. |
[7.SP.1] Understand that generalizations about a population from a sample are valid only if the sample is representative of that population. |
Downstream impacted | Grade 7 |
| 39. |
[7.SP.1] Understand that random sampling tends to produce representative samples and support valid inferences. |
Downstream impacted | Grade 7 |
| 40. |
[7.SP.2] Use data from a random sample to draw inferences about a population with an unknown characteristic of interest. |
Downstream impacted | Grade 7 |
| 41. |
[7.SP.2] Generate multiple samples (or simulated samples) of the same size to gauge the variation in estimates or predictions. |
Downstream impacted | Grade 7 |
| 42. |
[7.SP.3] Informally assess the degree of visual overlap of two numerical data distributions with similar variabilities, measuring the difference between the centers by expressing it as a multiple of a measure of variability. |
Downstream impacted | Grade 7 |
| 43. |
[7.SP.4] Use measures of center and measures of variability for numerical data from random samples to draw informal comparative inferences about two populations. |
Downstream impacted | Grade 7 |
| 44. |
[8.G.6] Explain a proof of the Pythagorean Theorem and its converse. |
Downstream impacted | Grade 8 |
| 45. |
[8.G.7] Apply the Pythagorean Theorem to determine unknown side lengths in right triangles |
Downstream impacted | Grade 8 |
| 46. |
[8.G.8] Apply the Pythagorean Theorem to find the distance between two points in a coordinate system. |
Downstream impacted | Grade 8 |
| 47. |
[G-C.2] Identify and describe relationships among inscribed angles, radii, and chords |
Downstream impacted | High School |
| 48. |
[G-C.3] Construct the inscribed and circumscribed circles of a triangle |
Downstream impacted | High School |
| 49. |
[G-C.3] Prove properties of angles for a quadrilateral inscribed in a circle |
Downstream impacted | High School |
| 50. |
[G-C.4] Construct a tangent line from a point outside a given circle to the circle. |
Downstream impacted | High School |
| 51. |
[G-GPE.1] Derive the equation of a circle of given center and radius |
Downstream impacted | High School |
| 52. |
[G-GPE.1] Complete the square to find the center and radius of a circle given by an equation. |
Downstream impacted | High School |
| 53. |
[G-GPE.2] Derive the equation of a parabola given a focus and directrix. |
Downstream impacted | High School |
| 54. |
[G-GPE.3] Derive the equation of hyperbola given the foci. |
Downstream impacted | High School |
| 55. |
[G-GPE.3] Derive the equation of ellipse given the foci. |
Downstream impacted | High School |
| 56. |
[G-GPE.4] Use coordinates to prove simple geometric theorems algebraically. |
Downstream impacted | High School |
| 57. |
[G-GPE.5] Prove the slope criteria for parallel and perpendicular lines |
Downstream impacted | High School |
| 58. |
[G-GPE.5] Use the slope criteria for parallel and perpendicular lines to solve geometric problems. |
Downstream impacted | High School |
| 59. |
[G-GPE.6] Find the point on a directed line segment between two given points that partitions the segment in a given ratio. |
Downstream impacted | High School |
| 60. |
[G-GPE.7] Use coordinates to compute perimeters of polygons and areas of triangles and rectangles |
Downstream impacted | High School |
| 61. |
[G-SRT.9] Derive the formula for the area of a triangle by drawing an auxiliary line from a vertex perpendicular to the opposite side. |
Downstream impacted | High School |
| 62. |
[S-ID.1] Represent data with plots on the real number line (dot plots, histograms, and box plots). |
Downstream impacted | High School |
| 63. |
[S-ID.2] Use statistics appropriate to the shape of the data distribution to compare center and spread of two or more different data sets. |
Downstream impacted | High School |
| 64. |
[S-ID.3] Interpret differences in shape, center, and spread in the context of the data sets, accounting for possible effects of extreme data points (outliers). |
Downstream impacted | High School |